PROBLEMAS DE ASIGNACIÓN
PROBLEMAS DE ASIGNACIÓN
El problema de asignación es una variación del problema original de transporte, variación en la cual las variables de decisión X(i,j) solo pueden tomar valores binarios, es decir ser cero (0) o uno (1), en la solución óptima, lo que supone que la oferta y la demanda están perfectamente alineadas, de hecho ambas son iguales a uno (1).
Múltiples son los casos en los que como ingenieros industriales podemos hacer uso del problema de asignación para resolver diversas situaciones, entre los que cabe mencionar se encuentran la asignación de personal a maquinas, herramientas a puestos de trabajos, horarios a maestros, candidatos a vacantes, huéspedes a habitaciones, comensales a mesas, vendedores a zonas territoriales etc.
En el modelo de asignación, la idea fundamental de resolución es ¿qué fuente satisface mejor el destino?, y dado que hemos asociado el modelo a una gran diversidad de circunstancias esta pregunta puede plantearse en múltiples contextos, como ¿qué candidato es el idóneo para la vacante?, o ¿qué personal es el indicado para la línea productiva?, o ¿qué personal es el mejor para ejecutar determinada tarea?. Una característica particular del modelo de asignación es que para su resolución no se hace necesario que el número de fuentes sea igual al número de destinos, lo cual es muy común en la vida real, teniendo en cuenta su aplicación, pues generalmente la cantidad de aspirantes es superior al número de vacantes (lógicamente haciendo referencia a la aplicación del modelo al contexto de oferta y demanda laboral).
El modelo de asignación es un tipo especial de problema de programación lineal en el que los asignados son recursos que se destinan a la realización de tareas. Por ejemplo, los asignados pueden ser empleados a quienes se tiene que dar trabajo. La asignación de personas a trabajos es una aplicación común del problema de asignación. Sin embargo, los asignados no tienen que ser personas. También pueden ser máquinas, vehículos o plantas, o incluso periodos a los que se asignan tareas.
“La mejor persona para el puesto” es una buena descripción del modelo de asignación.
El objetivo del modelo es determinar la asignación óptima (de costo mínimo) de trabajadores a puestos.
El modelo general de asignación con n trabajadores y n puestos se representa en la tabla siguiente:
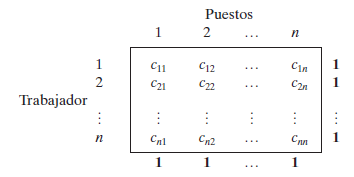
Para que se ajuste a la definición de un problema de asignación, es necesario que este tipo de aplicaciones se formule de manera tal que se cumplan los siguientes supuestos:
- El número de asignados es igual al número de tareas. (Este número se denota por n.)
- A cada asignado se le asigna sólo una tarea.
- Cada tarea debe realizarla sólo un asignado.
- Existe un costo cij asociado con el asignado i (i 5 1, 2, . . . , n) que realiza la tarea j ( j 1, 2, . . . , n).
- El objetivo es determinar cómo deben hacerse las n asignaciones para minimizar los costos totales.
Se puede resolver el modelo de asignación en forma directa como modelo normal de transporte. Sin embargo, el hecho de que todas las ofertas y las demandas son iguales a 1, condujo al desarrollo de un algoritmo sencillo de solución llamado método húngaro.
MÉTODO HÚNGARO
Apartándonos un poco de la idea expresada en módulos anteriores respecto a la facilidad de resolver problemas atinentes a la investigación operativa en especial aquellos de transporte mediante el uso de herramientas tecnológicas como lo son WinQSB, LINGO, TORA, STORM, Excel etc.. vale la pena ya sea para fines académicos o de cultura ingenieril realizar la resolución del problema de asignación mediante el algoritmo que se creó para tal fin, como lo es el Método Húngaro.
El método Húngaro es un método de optimización de problemas de asignación, conocido como tal gracias a que los primeros aportes al método clásico definitivo fueron de Dénes König y Jenő Egerváry dos matemáticos húngaros. El algoritmo tal como se detallará a continuación está diseñado para la resolución de problemas deminimización únicamente, será entonces cuestión de agregar un paso adicional para abordar ejercicios de maximización.
ALGORITMO HÚNGARO, PASO 1
Antes que nada cabe recordar que el método húngaro trabaja en una matriz de costos n*m (en este caso conocida como matriz m*m, dado que el número de filas es igual al número de columnas n = m), una vez construida esta se debe encontrar el elemento más pequeño en cada fila de la matriz.
ALGORITMO HÚNGARO, PASO 2
Una vez se cumple el procedimiento anterior se debe construir una nueva matriz n*m, en la cual se consignarán los valores resultantes de la diferencia entre cada costo y el valor mínimo de la fila a la cual cada costo corresponde (valor mínimo hallado en el primer paso).
ALGORITMO HÚNGARO, PASO 3
Este paso consiste en realizar el mismo procedimiento de los dos pasos anteriores referidos ahora a las columnas, es decir, se halla el valor mínimo de cada columna, con la diferencia que este se halla de la matriz resultante en el segundo paso, luego se construirá una nueva matriz en la cual se consignarán los valores resultantes de la diferencia entre cada costo y el valor mínimo de la columna a la cual cada costo corresponde, matriz llamada "Matriz de Costos Reducidos".
ALGORITMO HÚNGARO, PASO 4
A continuación se deben de trazar líneas horizontales o verticales o ambas (únicamente de esos tipos) con el objetivo de cubrir todos los ceros de la matriz de costos reducidos con el menor número de líneas posibles, si el número de lineas es igual al número de filas o columnas se ha logrado obtener la solución óptima (la mejor asignación según el contexto de optimización), si el número de líneas es inferior al número de filas o columnas se debe de proceder con el paso 5.
ALGORITMO HÚNGARO, PASO 5
Este paso consiste en encontrar el menor elemento de aquellos valores que no se encuentran cubiertos por las lineas del paso 4, ahora se restará del restante de elementos que no se encuentran cubiertos por las líneas; a continuación este mismo valor se sumará a los valores que se encuentren en las intersecciones de las lineas horizontales y verticales, una vez finalizado este paso se debe volver al paso 4.
RESOLUCIÓN DE UN PROBLEMA DE ASIGNACIÓN MEDIANTE EL MÉTODO HÚNGARO
EL PROBLEMA
La compañía de manufactura "Jiménez y Asociados" desea realizar una jornada de mantenimiento preventivo a sus tres máquinas principales A, B y C. El tiempo que demanda realizar el mantenimiento de cada máquina es de 1 día, sin embargo la jornada de mantenimiento no puede durar más de un día, teniendo en cuenta que la compañía cuenta con tres proveedores de servicios de mantenimiento debe de asignarse un equipo de mantenimiento a cada máquina para poder cumplir con la realización del mantenimiento preventivo. Teniendo en cuenta que según el grado de especialización de cada equipo prestador de servicios de mantenimiento el costo de la tarea varía para cada máquina en particular, debe de asignarse el equipo correcto a la máquina indicada con el objetivo de minimizar el costo total de la jornada. Los costos asociados se pueden observar en la siguiente tabla:
PASO 1
Encontramos el menor elemento de cada fila
PASO 2
Construimos una nueva matriz con las diferencias entre los valores de la matriz original y el elemento menor de la fila a la cual corresponde.
PASO 3
En la matriz construida en el paso anterior se procede a efectuar el paso 1 esta vez en relación a las columnas, por ende escogemos el elemento menor de cada columna. Igualmente construimos una nueva matriz con la diferencia entre los valores de la matriz 2 y el elemento menor de la columna a la cual corresponde cada valor.
PASO 4
En este paso trazaremos la menor cantidad de combinaciones de líneas horizontales y verticales con el objetivo de cubrir todos los ceros de la matriz de costos reducidos.
Como se puede observar el menor número de líneas horizontales y/o verticales necesarias para cubrir los ceros de la matriz de costos reducidos es igual a 2, por ende al ser menor que el número de filas o columnas es necesario recurrir al paso 5.
PASO 5
En este paso seleccionamos el menor elemento de los elementos no subrayados.
Luego se procede a restarse de los elementos no subrayados y a adicionarse a los elementos ubicados en las intersecciones de las líneas, en este caso existe una única intersección (3).
Ahora ya efectuado este paso pasamos al paso 4.
Ahora observamos cómo se hace necesario trazar tres líneas (la misma cantidad de filas o columnas de la matriz) por ende se ha llegado al tabulado final, en el que por simple observación se determina las asignaciones óptimas.
Por ende la asignación que representa el menor costo para la jornada de mantenimiento preventivo determina que el Equipo 1 realice el mantenimiento de la Máquina 1, el Equipo 2 realice el mantenimiento de la Máquina 3 y el Equipo 3 realice el mantenimiento de la Máquina 2, jornada que tendrá un costo total de 17 unidades monetarias.










gran aporte! gracias
ResponderBorrar