Formulación De Modelos

            

                                      Formulación de Modelos

Formulación de Modelos de Programación Lineal

Elementos básicos de un modelo matemático

Un modelo matemático es producto de la abstracción de un sistema real, eliminando las complejidades y haciendo suposiciones pertinentes; se aplica una técnica matemática y se obtiene una representación simbólica del mismo.

Un modelo matemático consta al menos de tres elementos o condiciones básicas: Las Variables de decisión, la Función Objetivo y las Restricciones.

• Variables de decisión y parámetros

Las variables de decisión son incógnitas que deben ser determinadas a partir de la solución del modelo. Los parámetros representan los valoresconocidos del sistema o que se pueden controlar. Las variables de decisión se representan por: X1, X2, X3,…, Xn ó Xi, i = 1, 2, 3,…, n.

• Función Objetivo

La función objetivo es una relación matemática entre las variables de decisión, parámetros y una magnitud que representa el objetivo o producto del sistema. Es la medición de la efectividad del Modelo formulado en función de las variables. Determina lo que se va optimizar (Maximizar o Minimizar).

La solución ÓPTIMA se obtiene cuando el valor de la Función Objetivo es óptimo (valor máximo o mínimo), para un conjunto de valores factibles de las variables. Es decir, hay que reemplazar las variables obtenidas X1, X2, X3,…, Xn; en la Función Objetivo Z = f (C1X1, C2X2, C3X3,…, CnXn) sujeto a las restricciones del modelo matemático.

Por ejemplo, si el objetivo es minimizar los costos de operación, la función objetivo debe expresar la relación entre el costo y las variables de decisión, siendo el resultado el menor costo de las soluciones factibles obtenidas.

• Restricciones

Las restricciones son relaciones entre las variables de decisión y los recursos disponibles. Las restricciones del modelo limitan el valor de las variables de decisión. Se generan cuando los recursos disponibles son limitados.

En el Modelo se incluye, adicionalmente de las restricciones, la Restricción de No Negatividad de las Variables de decisión, o sea: Xi = 0.

La programación lineal es la interrelación de los componentes de un sistema, en términos matemáticos, ya sea en forma de ecuaciones o inecuaciones lineales llamado Modelo de Programación Lineal. Es una técnica utilizada para desarrollar modelos matemáticos, diseñada para optimizar el uso de los recursos limitados en una empresa u organización.

El Modelo de Programación Lineal, es una representación simbólica de la realidad que se estudia, o del problema que se va a solucionar. Se forma con expresiones de lógicas matemáticas, conteniendo términos que significan contribuciones: a la utilidad (con máximo) o al costo (con mínimo) en la Función Objetivo del modelo. Y al consumo de recursos disponibles (con desigualdades = ó = e igualdades =) en las restricciones.

En el presente texto desarrollaremos Modelos Matemáticos de Programación Lineal de: Maximización y Minimización, los cuales estarán indicados en la Función Objetivo del Modelo.

Aplicación a la Formulación de los Modelos de Investigación de operaciones

(a) Modelo Matemático: Se emplea cuando la función objetivo y las restricciones del modelo se pueden expresar en forma cuantitativa o matemática como funciones de las variables de decisión.

(b) Modelo de Simulación: Los modelos de simulación difieren de los matemáticos en que las relación entre la entrada y la salida no se indican en forma explícita. En cambio, un modelo de simulación divide el sistema representado en módulos básicos o elementales que después se enlazan entre si vía relaciones lógicas bien definidas. Por lo tanto, las operaciones de cálculos pasaran de un módulo a otro hasta que se obtenga un resultado de salida.

Los modelos de simulación cuando se comparan con modelos matemáticos; ofrecen mayor flexibilidad al representar sistemas complejos, pero esta flexibilidad no esta libre de inconvenientes. La elaboración de este modelo suele ser costoso en tiempo y recursos. Por otra parte, los modelos matemáticos óptimos suelen poder manejarse en términos de cálculos.

Modelos de Investigación de Operaciones de la ciencia de la administración: Los científicos de la administración trabajan con modelos cuantitativos de decisiones.

Modelos Formales: Se usan para resolver problemas cuantitativos de decisión en el mundo real. Algunos modelos en la ciencia de la administración son llamados modelos deterministicos. Esto significa que todos los datos relevantes (es decir, los datos que los modelos utilizarán o evaluarán) se dan por conocidos. En los modelos probabilísticos (o estocásticos), alguno de los datos importantes se consideran inciertos, aunque debe especificarse la probabilidad de tales datos.

En la siguiente tabla se muestran los modelos de decisión según su clase de incertidumbre y su uso en las corporaciones. (D, determinista; P, probabilista; A, alto; B, bajo)

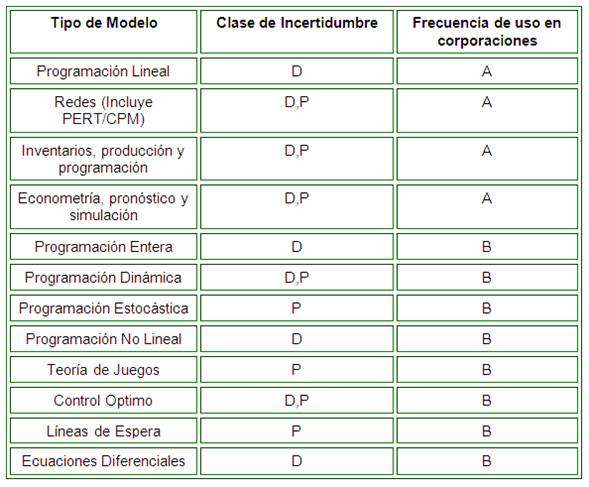
Modelo de Hoja de Cálculo Electrónica: La hoja de cálculo electrónica facilita hacer y contestar preguntas de "que si" en un problema real. Hasta ese grado la hoja de cálculo electrónica tiene una representación selectiva del problema y desde este punto de vista la hoja de cálculo electrónica es un modelo.

En realidad es una herramienta más que un procedimiento de solución. 

Problemas de aplicación para formular un modelo

1). Proceso de producción.- Una fábrica produce dos tipos de productos: M y N, los costos de producción de ambos productos son $3 para el producto M y $5 para el producto N. El tiempo total de producción está restringido a 500 horas; y los tiempos de producción son de 8 horas/unidad para el producto M y de 4 horas/unidad para el producto N. Formule el Modelo matemático que permita determinar la cantidad de productos M y N a producir, y que optimice el Costo total de producción de los dos productos.

Formulación del Modelo

En la formulación del modelo, podemos ayudarnos con la representación del Problema mediante un organizador gráfico o esquema:

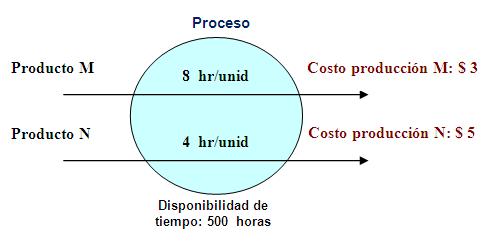
• Definición de Variables

Se desea formular un modelo matemático para determinar la cantidad que debe producirse por cada producto (M y N), por lo tanto tendremos dos variables, representados por: x1 , x2.

Siendo: x1 = Cantidad a producirse del producto M,

x2 = Cantidad a producirse del producto N

• Función Objetivo

Como se tiene información de Costos de producción de los productos M y N, el objetivo será minimizarlos:

Luego la Función Objetivo será Minimizar "C" igual al Costo total de producción del producto M más el Costo total de producción del producto N.

Matemáticamente la Función Objetivo es:

• Definición de Restricciones

El tipo de recurso en el problema es el tiempo (puede ser horas hombre u horas máquina). Formulamos la restricción, colocando en el lado izquierdo de la inecuación el consumo unitario de los productos M y N, y en el lado derecho la cantidad disponible del recurso (500 horas).

Resumiendo tenemos el siguiente Modelo matemático de Programación Lineal del Problema (un modelo con dos variables y una restricción, estando listo para aplicar un método de solución:

 Caso de toma de decisiones

alternativas de fabricación se desarrollan en las restricciones del Modelo matemático; y la toma de 

decisiones se determina evaluando en la Función objetivo las alternativas obtenidas.

Bibliografia:

https://www.monografias.com/trabajos96/formulacion-modelos-programacion-lineal/formulacion-modelos-programacion-lineal.shtml

MAPA CONCEPTUAL

Referencia: https://sites.google.com/site/optilineal2404/introduccion

VIDEO

Ejemplo

Referencia: https://www.youtube.com/watch?v=05KxQCULaRI