EJEMPLO DE MAXIMIZAR Y MINIMIZAR CON DERVADAS
Problema 1
Se quiere construir una caja sin tapa a partir de una hoja de cartón de 20x10cm. Para ello, se corta un cuadrado de lado L en cada esquina y se dobla la hoja levantando los cuatro laterales de la caja.
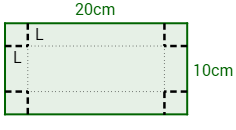
Determinar las dimensiones de la caja para que su volumen sea máximo si el lado debe medir entre 2 y 3 cm ().
Solución
Si es el ancho de la caja, es su altura y es su profundidad, entonces su volumen es
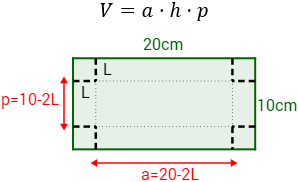 Al cortar los cuatro cuadrados de lado , el ancho de la caja es
Al cortar los cuatro cuadrados de lado , el ancho de la caja es
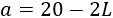 La profundidad es
La profundidad es
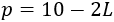 Por último, la altura coincide con el lado del cuadrado recortado:
Por último, la altura coincide con el lado del cuadrado recortado:
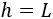 Luego el volumen de la caja en función de es (paso 1)
Luego el volumen de la caja en función de es (paso 1)
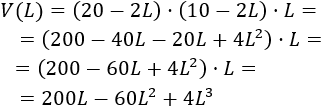 Derivamos la función volumen (paso 2):
Derivamos la función volumen (paso 2):
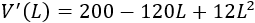 Igualamos a 0 la derivada y resolvemos la ecuación para encontrar los puntos críticos (paso 3):
Igualamos a 0 la derivada y resolvemos la ecuación para encontrar los puntos críticos (paso 3):
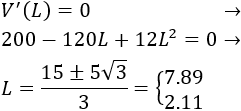 Situamos los puntos en la recta real y estudiamos los signos en los intervalos (paso 4):
Situamos los puntos en la recta real y estudiamos los signos en los intervalos (paso 4):
 Escogemos los puntos del primer intervalo, del segundo intervalo y del tercero:
Escogemos los puntos del primer intervalo, del segundo intervalo y del tercero:
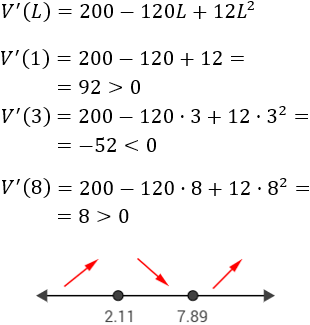 Luego la función es creciente en el primer intervalo, decreciente en el segundo y creciente en el tercero:
Luego la función es creciente en el primer intervalo, decreciente en el segundo y creciente en el tercero:
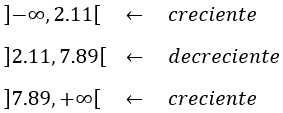 Pero el lado debe medir entre 2 y 3, es decir, debe ser
Pero el lado debe medir entre 2 y 3, es decir, debe ser
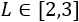 Como en el intervalo la función es decreciente, el volumen será máximo para .
Como en el intervalo la función es decreciente, el volumen será máximo para .
Por tanto, las dimensiones de la caja deben ser
 Es decir, las dimensiones son 15.78 x 5.78 x 2.11 cm y su volumen es .
Es decir, las dimensiones son 15.78 x 5.78 x 2.11 cm y su volumen es .
Problema 3
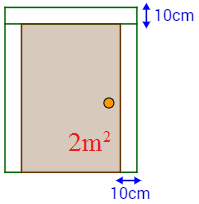
Una empresa de fabricación de puertas de madera utiliza un tablón rectangular para la hoja y tres listones de 10cm de ancho para el marco (lados laterales y lado superior). El precio del tablón es de $128 por metro cuadrado y el de los listones es de $87 por metro lineal.
 Calcular:
Calcular:

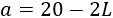
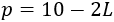
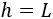
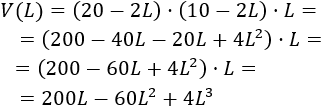
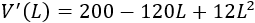
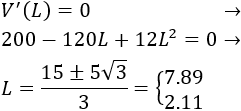

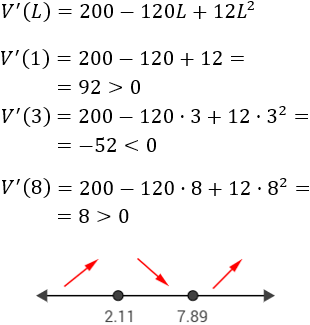
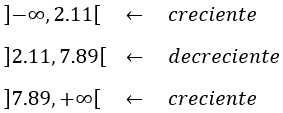
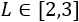
Por tanto, las dimensiones de la caja deben ser

Problema 2
Una empresa vende 0.7 toneladas de zumo y 0.3 toneladas de sobrante por cada tonelada de materia prima. El coste de la materia prima es de 0.8€/kg, los precios de venta del zumo y del sobrante son 2.5€/kg y 0.05€/kg, respectivamente, y el coste de producción viene dado por la función
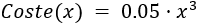 donde representa las toneladas de zumo producido.
donde representa las toneladas de zumo producido.
Obtener:
Una empresa vende 0.7 toneladas de zumo y 0.3 toneladas de sobrante por cada tonelada de materia prima. El coste de la materia prima es de 0.8€/kg, los precios de venta del zumo y del sobrante son 2.5€/kg y 0.05€/kg, respectivamente, y el coste de producción viene dado por la función
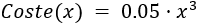
Obtener:
- Una expresión para calcular las ganancias netas en función de las toneladas de materia prima.
- La cantidad de zumo que se debe fabricar para que las ganancias netas sean máximas.
Solución
Sea la cantidad de materia prima y sean y las cantidades de zumo y de sobrante, respectivamente.
El número de toneladas de zumo producido en función de las toneladas de materia prima es
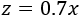 Y el de sobrante,
Y el de sobrante,
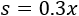 Las ganancias brutas son:
Las ganancias brutas son:
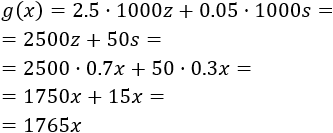 Hemos multiplicado por 1000 porque el precio es por kilo y no por tonelada.
Hemos multiplicado por 1000 porque el precio es por kilo y no por tonelada.
El coste total es el coste de la materia prima más el coste de producción:
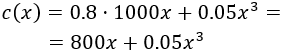 Luego las ganancias netas en función de las toneladas de materia prima son:
Luego las ganancias netas en función de las toneladas de materia prima son:
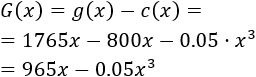 Calculamos la derivada:
Calculamos la derivada:
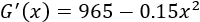 Igualamos la derivada a 0 y resolvemos la ecuación para buscar puntos críticos:
Igualamos la derivada a 0 y resolvemos la ecuación para buscar puntos críticos:
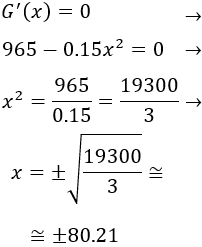 Representamos los puntos obtenidos en la recta real y estudiamos el signo de la derivada:
Representamos los puntos obtenidos en la recta real y estudiamos el signo de la derivada:
 Elegimos el punto del primer intervalo, el punto del segundo y el punto del tercer intervalo:
Elegimos el punto del primer intervalo, el punto del segundo y el punto del tercer intervalo:
 Por el criterio de la primera derivada, la función es decreciente en el primer y tercer intervalo y creciente en el segundo:
Por el criterio de la primera derivada, la función es decreciente en el primer y tercer intervalo y creciente en el segundo:
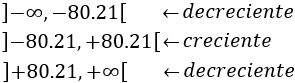 Nota: podemos acotar el dominio de la función al intervalo de los reales positivos ya que no tiene sentido que se produzcan cantidades negativas de zumo.
Nota: podemos acotar el dominio de la función al intervalo de los reales positivos ya que no tiene sentido que se produzcan cantidades negativas de zumo.
De la monotonía, deducimos que en el punto la función tiene un mínimo y en el punto tiene un máximo.
Por tanto, las ganancias netas son máximas cuando la cantidad de materia prima es 80.21 toneladas. En toneladas de zumo, equivale a 56.15 toneladas ya que
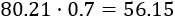
El número de toneladas de zumo producido en función de las toneladas de materia prima es
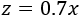
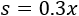
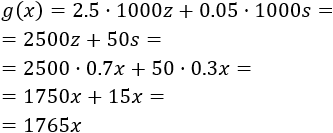
El coste total es el coste de la materia prima más el coste de producción:
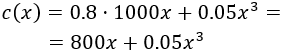
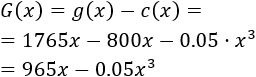
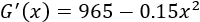
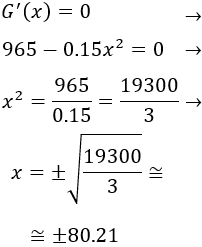


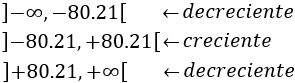
De la monotonía, deducimos que en el punto la función tiene un mínimo y en el punto tiene un máximo.
Por tanto, las ganancias netas son máximas cuando la cantidad de materia prima es 80.21 toneladas. En toneladas de zumo, equivale a 56.15 toneladas ya que
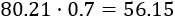
Problema 3
Una empresa de fabricación de puertas de madera utiliza un tablón rectangular para la hoja y tres listones de 10cm de ancho para el marco (lados laterales y lado superior). El precio del tablón es de $128 por metro cuadrado y el de los listones es de $87 por metro lineal.

- Las dimensiones de una puerta de de superficie de hoja para que el coste sea mínimo. ¿Cuál será su precio?
- Si la puerta es de 2.5 metros de ancho y 0.8 metros de alto, ¿cuál es su precio?
Solución
Sean e la anchura y altura de la hoja de la puerta, respectivamente. Como la superficie de la hoja es , tenemos que
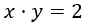 Como la anchura de los listones es de 10cm, la longitud del listón del lado superior debe ser (escribimos 0.1 ya que los precios son por metro)
Como la anchura de los listones es de 10cm, la longitud del listón del lado superior debe ser (escribimos 0.1 ya que los precios son por metro)
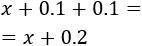 La longitud de los dos listones de los lados laterales debe ser
La longitud de los dos listones de los lados laterales debe ser
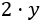 El coste total es el coste de la hoja más el del marco. El coste de la hoja es
El coste total es el coste de la hoja más el del marco. El coste de la hoja es
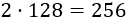 El coste del listón superior es
El coste del listón superior es
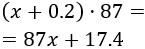 Y el coste de los listones laterales es
Y el coste de los listones laterales es
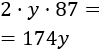 Por tanto, el coste total es
Por tanto, el coste total es
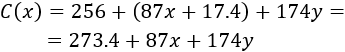 Como tenemos dos variables, escribimos en función de :
Como tenemos dos variables, escribimos en función de :
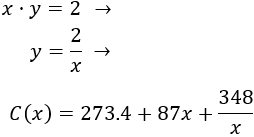 Calculamos la derivada:
Calculamos la derivada:
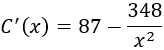 Igualamos a 0 y resolvemos la ecuación para buscar los puntos críticos:
Igualamos a 0 y resolvemos la ecuación para buscar los puntos críticos:
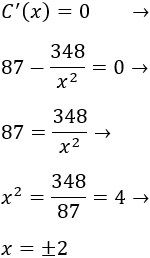 Situamos los puntos críticos en la recta real y estudiamos el signo de la derivada en los 4 intervalos:
Situamos los puntos críticos en la recta real y estudiamos el signo de la derivada en los 4 intervalos:
 Nota: hay que incluir el punto como punto crítico ya que la función no está definida en dicho punto (no se puede dividir entre 0).
Nota: hay que incluir el punto como punto crítico ya que la función no está definida en dicho punto (no se puede dividir entre 0).
Escogemos para el primer intervalo, para el segundo, para el tercero y para el cuarto:
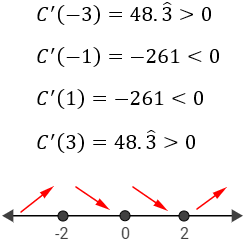 La función es creciente para , decreciente en el intervalo y creciente para . Además, tiene un en .
La función es creciente para , decreciente en el intervalo y creciente para . Además, tiene un en .
Nota: cuando tiende a la función decrece, pero como representa una longitud, debe ser positiva.
Las dimensiones son
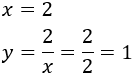 Es decir, 2 metros de ancho y 1 de alto.
Es decir, 2 metros de ancho y 1 de alto.
Calculamos el coste:
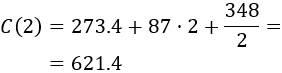 Luego el coste total de la puerta es $621.4.
Luego el coste total de la puerta es $621.4.
Apartado b:
Evaluando la función en (),
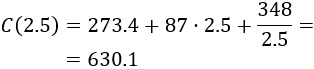
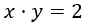
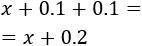
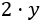
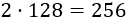
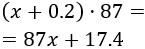
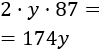
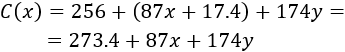
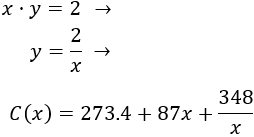
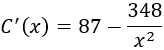
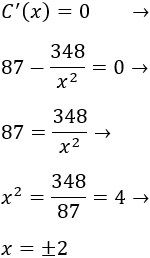

Escogemos para el primer intervalo, para el segundo, para el tercero y para el cuarto:

Nota: cuando tiende a la función decrece, pero como representa una longitud, debe ser positiva.
Las dimensiones son
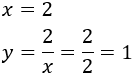
Calculamos el coste:
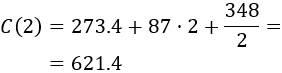
Apartado b:
Evaluando la función en (),
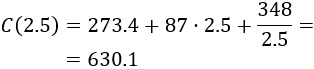

Comentarios
Publicar un comentario