APLICACIÓN DE PROGRAMACIÓN LINEAL
APLICACIÓN DE PROGRAMACIÓN LINEAL
§La programación lineal es un método
eficiente para determinar una decisión óptima entre un gran número de
decisiones posibles
§Es impresionante el número y la
diversidad de problemas en los que se puede aplicar.

IMÁGENES
IMÁGENES
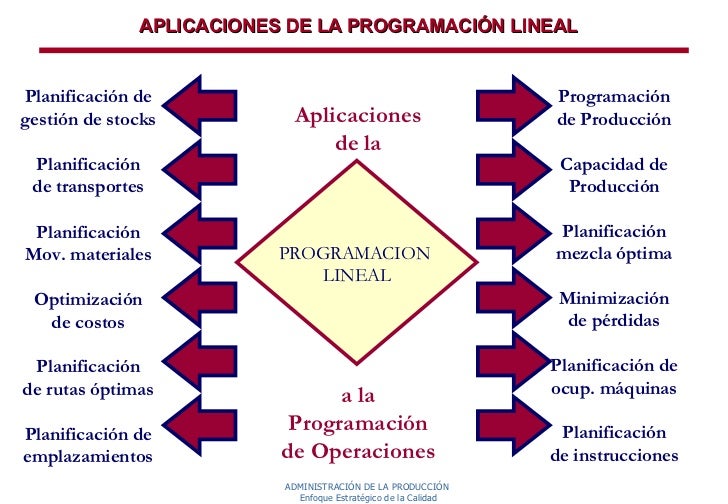
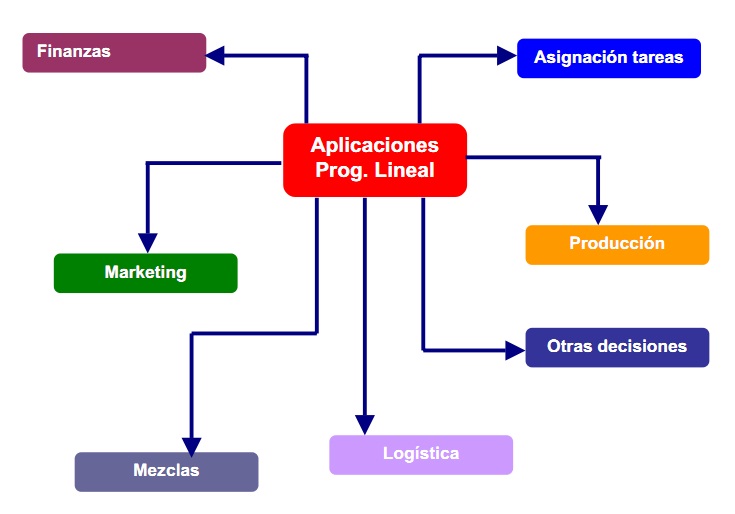
Clasificación de las aplicaciones de PL
La Programación Lineal presenta un gran número de aplicaciones en multitud de
ámbitos empresariales, industriales, de gestión y en general, de toma de
decisiones.
EJEMPLO
Problema de Inversión: Considere que usted dispone de un capital de 21.000 dólares para invertir en la bolsa de valores. Un amigo le recomienda 2 acciones que en el último tiempo han estado al alza: Acción A y Acción B. La Acción A tiene una rentabilidad del 10% anual y la Acción B del 8% anual. Su amigo le aconseja tener una cartera equilibrada y diversa y por tanto le recomienda invertir un máximo de 13.000 dólares en la Acción A y como mínimo 6.000 dólares en la Acción B. Además la inversión en la Acción A debe ser menor o igual que el doble de la inversión destinada a la Acción B. Usted quiere formular y resolver un modelo de Programación Lineal que permita obtener la política de inversión que permita obtener la máxima rentabilidad (interés) anual.
Variables de Decisión:
x = dólares invertidos en Acción A.
y = dólares invertidos en Acción B.
x = dólares invertidos en Acción A.
y = dólares invertidos en Acción B.
Función Objetivo: Se busca maximizar la rentabilidad anual que resulta de invertir en los 2 tipos de acciones.
Maximizar 0.1x + 0.08y
Maximizar 0.1x + 0.08y
Restricciones: Considera las recomendaciones de su amigo.
| x + y ≤ 21.000 | Se puede invertir como máximo 21.000 dólares en total |
| x ≤ 13.000 | Invertir como máximo 13.000 dólares en Acción A |
| y ≥ 6.000 | Invertir como mínimo 6.000 dólares en Acción B |
| x - 2y ≤ 0 | Inversión en A debe ser menor o igual que el doble de la inversión en B |
| x≥0, y≥0 | No Negatividad |
Sólución Óptima: X = 13.000 Y = 8.000. Valor Óptimo V(P) = 1.940 dólares.
Problema de Proceso Productivo: Una empresa produce tres tipos de muebles (A, B y C), cada uno de los cuales se vende a $200, $150 y $120 respectivamente. Para la producción de estos muebles la empresa cuenta con 315 horas disponibles en un taller de corte de madera, 110 horas disponibles en un taller de lijado y 50 horas en un taller de pintado. Se ha estimado que el mueble A requiere por unidad 15 horas de trabajo en el taller de corte, 2 horas en el taller de lijado y 1 hora en el taller de pintado (estos mismos valores para los muebles B y C son 7,5:3:1 y 5:2:1, respectivamente). Se requiere formular y resolver un modelo de Programación Lineal que permita encontrar la cantidad a elaborar y vender de estos muebles de modo que la empresa obtenga el mayor beneficio.
Variables de Decisión:
X = Unidades a elaborar y vender del mueble A.
Y = Unidades a elaborar y vender del mueble B.
Z = Unidades a elaborar y vender del mueble C.
X = Unidades a elaborar y vender del mueble A.
Y = Unidades a elaborar y vender del mueble B.
Z = Unidades a elaborar y vender del mueble C.
De esta forma el modelo de optimización que permite encontrar el plan óptimo de producción es el siguiente:
Problema de Mezcla de Productos: Se dispone de 2 ingredientes para fabricar caramelos, cuyo sabor variará dependiendo de la proporción en que intervengan cada uno de los ingredientes. El primer ingrediente se compra a $10 por kg. y el segundo a $20 por kg. El proceso de elaboración supone un costo de $5 por kg. fabricado, cuya cantidad total corresponde simplemente a la suma de los kg. empleados en la mezcla. La demanda máxima para un mes se cifra en 100 kg y el precio de venta $50 kg. A la empresa no le interesa producir más de los que puede vender en el mes. Por último, la composición de la masa debe contener una proporción que no supere el 50% del primer ingrediente y el 80% del segundo ingrediente. Se requiere determinar cuántos kg. de caramelos se tiene que fabricar al mes y las proporciones en las que deben ser utilizados los ingredientes para obtener un máximo beneficio.
Variables de Decisión:
X1: Kg a usar del ingrediente 1 en un mes
X2: Kg a usar del ingrediente 2 en un mes
X1: Kg a usar del ingrediente 1 en un mes
X2: Kg a usar del ingrediente 2 en un mes
Función Objetivo: Obtener la maxima utilidad de la venta de los caramelos descontando los costos de producción
Maximizar 50*(X1 + X2) – 10*X1 – 20*X2 - 5*(X1 + X2) = 35*X1 + 25*X2
Maximizar 50*(X1 + X2) – 10*X1 – 20*X2 - 5*(X1 + X2) = 35*X1 + 25*X2
Restricciones:
Demanda Máxima: X1 + X2 <= 100
Composición: X1/(X1 + X2) <= 50% o 0,5*X1 – 0,5*X2 <= 0
Composición: X2/(X1 + X2) <= 80% o -0,8*X1 + 0,2*X2 <= 0
No Negatividad: X1,X2>=0
Demanda Máxima: X1 + X2 <= 100
Composición: X1/(X1 + X2) <= 50% o 0,5*X1 – 0,5*X2 <= 0
Composición: X2/(X1 + X2) <= 80% o -0,8*X1 + 0,2*X2 <= 0
No Negatividad: X1,X2>=0
Sólución Óptima: X1 = 50 X2 = 50. Valor Óptimo V(P) = $3.000.
VÍDEO

EMPRESA DE MEDICINAS
ResponderBorrarUna empresa dedicada a la fabricación de MEDICI NAS, necesita para la elaboración de un nuevo
medicamento un determinado componente. Si
decide comprar dicho componente a otro labora torio deberá pagar un precio de 5.180 dólar por
componente. Si decide producirlo ella misma incu rriría en unos costos fijos anuales de 15 020 dóla res, siendo el costo variable de cada componente 3.678 dólar. Se pide:
a) ¿Para qué volumen de unidades anuales de este componente a la empresa le es
indiferente comprarlo o fabricarlo?
b) Representa gráficamente la solución a la pregunta anterior
c) Si prevé unas necesidades de 15 componentes, ¿qué decisión adoptaría? Razona
la respuesta. me ayudan en esto por favor
La empresa “Cuerpo feliz” produce dos modelos de caminadoras. La fabricación de cada modelo de lujo requiere 15 libras de plástico y 12 minutos de trabajo. La producción de cada modelo estándar requiere 20 libras de plástico y 14 minutos de trabajo. La ganancia por cada modelo de lujo es $20 y $35 por cada modelo estándar. Si se dispone de 8000 libras de plástico y 120 horas de trabajo para la producción diaria de caminadoras. ¿Cuántas unidades de cada modelo hay que producir para maximizar las ganancias?
ResponderBorrarFormule un modelo matemático para determinar la mejor estrategia de envío incurriendo en el mínimo costo. Deben definir variables, Función objetivo, y restricciones.
Deben definir variables:
Función objetivo.
Restricciones
Solución óptima
Una fábrica produce dos tipos de refrescos de alcachofa I, II los cuales se venden a 12 Bs y 8 Bs, el litro respectivamente,
ResponderBorrarla empresa tiene diversos recursos limitados humanos – tecnológicos y de capital ya que se dispone de 12 horas de
trabajo hombre – máquina por día y de un capital máximo de producción de 28000 Bs por día se estima que para
producir mil litros del refresco I, se requiere de 4 horas de trabajo y para producir el refresco II solo 2 horas de trabajo. El
costo de producción de mil litros del refresco I es de 7000 Bs y el costo de producción mil litros del refresco II es de 8000
Planteamiento:
BorrarFabrica de Muebles:
Precios Mano
en soles: Obra: Materiales: Impuestos
Producto A 12.000 1200 4.200 4,5%
Producto B 15.000 1500 4.400 5%
2700 8600
Topes de Inversión: 360000 Mano de Obra
52000 Matriales
58.000 Impuestos
X. Cantidad a fabricar del producto A
Y: cantidad a fabricar del producto B
Mano de Obra:
1200X + 1500Y = 360000
Materiales
4200X + 4400Y = 52000
Impuestos:
540 X + 750Y = 58.000
Ventas - Costos de Producción - Impuestos = Utilidad
a) ¿Cuál será la cantidad de cada producto que se deben fabricar para maximizar la ganancia?
Utilidad = 0,6 (12000X+ 15000Y) Para una ganancia del 60%
Ventas - Costos de Producción - Impuestos = Utilidad
X*12000 + 15000Y - 360.000- 52000-58000 = 0,6 (12000X+ 15000Y)
En una fábrica de planchas para el hogar, se requieren switches para cambiar
ResponderBorrarde velocidades de la licuadora, a una razón de 280 unidades diarias que se
piden en forma periódica, según la planeación de producción realizada. El
costo de la orden es de 560 pesos el iniciar dicha orden de compra, se estima
que una unidad de switch cuesta 0.015 centavos diarios. El tiempo de entrega
entre la colocación y la recepción de un pedido es de 20 días. Determine la
política óptima de inventario para pedir las luces.
la Industria del Plástico S. A. fabrica tubos de plástico de 6 m de longitud y contenedores de agua o tinas de 0,02
ResponderBorrarm3 (o su equivalente, 20 litros). El polietileno es el material principal utilizado en la fabricación de estos dos productos. Se
requieren 0,665 de polietileno para fabricar 6 m de longitud de tubo, y 0,3 kg para fabricar una tina. Diariamente se consumen
0,5 toneladas de polietileno. Para la fabricación de estos dos productos, se dispone de una máquina que trabaja
ininterrumpidamente 24h. al día, dedicando 1/10 hora/tina y 1/6 hora/tubo. La utilidad es $18 por cada tubo y $1,5 por c/tina
Una compañía fabrica y venden dos marcas de mascarillas M1 y M2.
ResponderBorrarPara su fabricación se necesita un trabajo manual de 8 minutos para el modelo M1 y de 12 minutos para el M2; y un trabajo de máquina de 3 minutos para el modelo M1 y de 2 minutos para 2.
Se dispone para el trabajo manual de 120 horas al mes y para la máquina 100 horas al mes. Sabiendo que el beneficio por unidad es de 2 y 3 dólares para M1 y M2, respectivamente, planificar la producción para obtener el máximo beneficio.
La colchonería Yako en Santiago produce colchones y almohadas. Se tiene informes de producción que reporta que para producir cada colchón toma 4 horas de mano de obra en el departamento de ensamblaje y 2 horas de acabado o terminación, mientras que para producir cada almohada requiere 3 horas de ensamblaje y 1 hora de terminaciones. Se tienen disponibles 240 horas de tiempo en el departamento de ensamblaje y 100 horas de tiempo en departamento de acabado. Al venderse la ganancia de cada colchón es de RD$70.00 y la ganancia de cada almohada es de RD$50.00.
ResponderBorrarBajo la pregunta de planificación: ¿Cuántos colchones y cuantas almohadas debe hacer la colchonería Yako para maximizar ganancias?
1) Por valor de 2 puntos: Plantear el problema de programación lineal por medio de modelo Matemática. ¡¡¡Recordar que son 4 etapas del modelado o planteamiento!!!
2) Por valor de 2 puntos: Presentar, por medio del método gráfico, la región o regiones factibles, con indicación clara hacia donde las rectas delimitan las regiones.
3) Por valor 3 puntos: Usando el Método Simplex y usando las tablas recomendadas en clases (imagen adjunta), busque solución a la meta que ha planteado o Función Objetivo que se ha solicitado.
Problema de Inversión: Considere que usted dispone de un capital de 21.000 dólares para invertir en la bolsa de valores. Un amigo le recomienda 2 acciones que en el último tiempo han estado al alza: Acción A y Acción B. La Acción A tiene una rentabilidad del 10% anual y la Acción B del 8% anual, ve a la siguiente página para más información
ResponderBorrar